Are your 4th or 5th grade students learning the array/area model for multiplying whole numbers? Do you find them having some struggles along the way and continuing to make common errors again and again? My students were having some trouble mastering the area model for multiplying whole numbers until I started asking them to "find my error!" Read all about how I started implementing error analysis into my multiplication unit with my 4th graders. 

Today's math hack is so simple, you can have it ready in 5 minutes--and you can use it for just about any concept you are teaching in math.

I have fallen in love with using Error Analysis with my 4th graders. 4th grade math content can be such a beast as students are required to master larger multiplication, division, and fraction concepts. Plus, they need to master their multiplication facts and become more accurate with all of their computation because almost everything requires multiple steps. In comes error analysis where students examine problems that have been completed with common errors. Students identify where the error was made and discuss what aspect of the concept the person who solved the problem does not quite understand.

During the second quarter, we focus on multiplication. I expect my students to master the area model and the standard algorithm. If you are unfamiliar with the area model for multiplication, here's a quick video that you can watch to understand how it works:

While I was teaching the multiplication area model, I kept noticing common errors (either within one student's work or across the class in general). Of course, this made me wonder what I had done wrong in my teaching and how I could go about improving students' understanding and mastery of the method.

I immediately thought of a way I could work with students' common errors by putting the mistakes on myself.

I decided to use students’ common errors to help them focus on becoming more accurate with multiplying whole numbers. I wanted my students to learn to look at their work more objectively and to have a way to help them revise any misunderstandings that they had internalized with their incorrect practice.

I grabbed some index cards and students' homework and started looking for errors. I came up with a handful of different errors they had made and created 5-6 cards. At the start of math, I displayed cards on the board with my document camera and asked students to raise their hands when they found my error. After a few practice problems together, I returned the students' homework and asked them to find their errors. I noticed a tremendous improvement in students' ability to find their errors and a greater focus on accuracy.

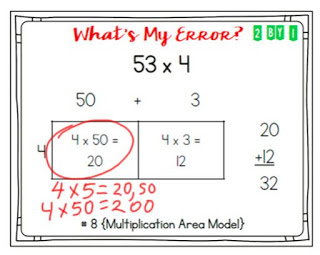
Now when students have an error on their paper, I say "Can you find your error? What's your error?" I love being able to call their mistakes an "error" and hope that they connect that word to the fun way I introduced it so that it's more like a game than a disappointment that their answer is not correct.

While we were identifying errors as a whole group, I realized that I would LOVE for students to work on identifying more errors made while using the area model to multiply and that task cards would be the perfect way to help every student practice and improve their own understanding of the area model. My "What's My Error?" task cards are now ready to go!!

Whether you are just now teaching students to multiply with the area model or have already taught your multiplication unit, these cards are perfect for spicing up your practice and review. My students actually love error analysis and were so engaged in trying to identify the error that had been made.

I will even be pulling these cards out soon for my 5th graders to help them review whole number multiplication! I think "What's My Error?" will be a hit with them as a fun way to make sure they remember how to use the area model to multiply. You can easily create your own error analysis task cards by taking a look at your students' errors, but it's so nice to have these sets ready to go now.

Multiplying Whole Numbers Error Analysis Task Cards

I ended up creating 80 error analysis task cards on 5 levels, so you have a variety of problems and can differentiate easily. Each card contains only 1 error. I expect students to find the correct answer after identifying the mistake that was made.

YOU CAN GET THE 3 DIGIT BY 1 DIGIT SET SENT TO YOUR INBOX TO TRY OUT WITH YOUR STUDENTS!

16 Task Cards are included for each of the following levels of multiplying whole numbers:

2 digit by 1 digit multiplication

3 digit by 1 digit multiplication

4 digit by 1 digit multiplication

2 digit by 2 digit multiplication

3 digit by 2 digit multiplication

Each set is color coded so that you can keep them separate, but if you don't print in color, I suggest that you print each set on different colors of cardstock to keep them organized. You can then assign students to the task card level that they need to work on for “instant” differentiated math!

What common multiplication errors did I include in these task cards?

• Student’s partial product does not have enough zeros when multiplying multiples of 10

• Student records too many zeros when multiplying multiples of 10

• Student does not line up place values correctly when adding the partial products to find the solution

• Student makes a multiplication fact error

• Student does not yet understand what parts of the factors to multiply and therefore multiplies a factor within itself vs multiplying by the other factor parts

• Student flips numbers when recording them to add the partial products

• Student did not expand numbers correctly when recording the hundreds/tens/ones

These cards connect to the Common Core Standards for 4th Grade Math.

4.NBT.5: Multiply a whole number of up to four digits by a 1-digit whole number, and multiply two 2-digit numbers, using strategies based on place value, the properties of operations, illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.